김채형 (Chaehyeong Kim)

김채형 (Chaehyeong Kim)

Archive

[NLP] 워드 임베딩 (Word Embedding) - Word2Vec

이 글은 워드 임베딩 방법론 중 Word2Vec에 관한 기록입니다.

1. 분산 표현 (Distributed Representation)

2. Word2Vec

Word2Vec은 단어 간 유사도를 계산할 수 있도록 단어의 의미를 반영하여 다차원 공간에 단어를 벡터화 하는 대표적인 방법 중 하나입니다. Word2Vec을 사용하면 다음과 같은 작업이 가능합니다.

고양이 + 애교 = 강아지
한국 - 서울 + 도쿄 = 일본

Word2Vec에서의 중심 단어(center word), 주변 단어(context word), 윈도우 크기(window size)는 다음과 같습니다.

  • 중심 단어 (centor word) : 중간에 있는 단어
  • 주변 단어 (context word) : 주변에 있는 단어
  • 윈도우 크기 (window size) : 앞뒤로 몇 개의 단어들을 주변 단어로 볼 것인지

Word2Vec에는 CBOW와 Skip-gram 두가지 방법이 존재합니다.

  • CBOW
    • 주변에 있는 단어들로 중간에 있는 단어들을 예측하는 방법
    • 주변 단어로 중심 단어를 예측하는 방법
  • Skip-gram
    • 중간에 있는 단어들로 주변에 있는 단어들을 예측하는 방법
    • 중심 단어로 주변 단어를 예측하는 방법

3. CBOW (Continuous Bag of Words)

3.1. CBOW 개념

CBOW는 주변에 있는 단어들로 중간에 있는 단어들을 예측하는 방법입니다. 이를 위해 주변 단어로 중심 단어를 예측합니다. CBOW에서의 중심 단어(center word), 주변 단어(context word), 윈도우 크기(window size)는 다음과 같습니다.

  • 중심 단어 (centor word) : 예측하고자 하는 단어
  • 주변 단어 (context word) : 예측하는 데에 사용되는 단어
  • 윈도우 크기 (window size) : 앞뒤로 몇 개의 단어들을 주변 단어로 볼 것인지
    • 즉 윈도우 크기가 $n$이면 앞쪽의 단어 $n$개와 뒤쪽의 단어 $n$개 총 $2n$개의 주변 단어들을 중심 단어를 예측하는 데에 사용

슬라이딩 윈도우 (Sliding Window)

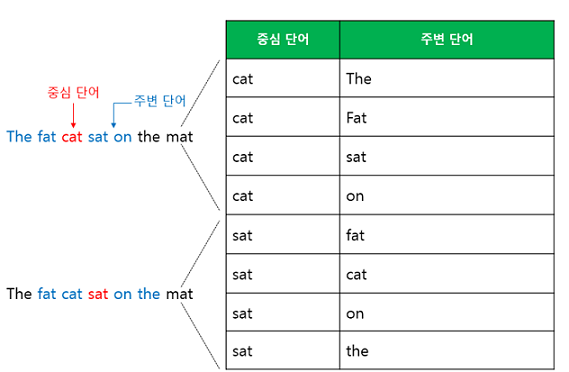
CBOW에서는 윈도우를 계속 움직이면서 중심 단어와 주변 단어 선택을 바꿔감으로써 학습을 위한 데이터셋을 만듭니다. 이를 슬라이딩 윈도우(sliding window)라고 합니다.

예를 들어 코퍼스에 아래와 같은 문장이 있다고 가정해봅시다.

예문 : “The fat cat sat on the mat”

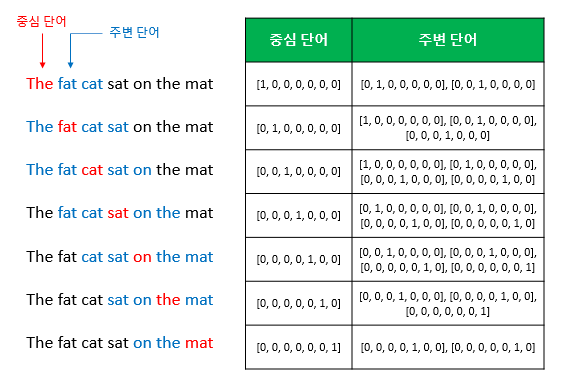
이때 슬라이딩 윈도우는 다음과 같이 이루어집니다.

3.2. CBOW 아키텍처

CBOW의 아키텍처는 다음과 같습니다.

위 그림에서 $V$는 one-hot vector의 차원을, $N$은 사용자가 설정한 embedded vector의 차원을 의미합니다.

  • $C$ : 단어의 개수
  • $V$ : one-hot vector의 차원
  • $N$ : embedded vector의 차원 (사용자 설정)

CBOW는 입력층(Input layer), 은닉층(Hidden layer), 출력층(Output layer)을 갖습니다. 각각의 차원은 다음과 같습니다.

  • 입력층 : $C \times V$ 차원
  • 은닉층 : $N$ 차원
  • 출력층 : $V$ 차원

입력층에는 사용자가 설정한 윈도우 크기 내 주변 단어들의 원-핫 벡터가, 출력층에는 중심 단어의 원-핫 벡터가 필요합니다. 은닉층(Hidden layer)은 투사층(Projection layer)이라고 불리기도 하는데, 룩업 테이블(Lookup table) 연산을 수행합니다.

CBOW에서 학습해야 하는 파라미터는 가중치 행렬 $W$와 $W’$입니다.

  • $W$ : 입력층과 은닉층 사이의 가중치 행렬 ($V \times N$ 행렬)
  • $W’$ : 은닉층과 출력층 사이의 가중치 행렬 ($N \times V$ 행렬)

이때 가중치 행렬 $W$와 $W’$는 같은 행렬을 전치(transpose)한 것이 아니라 서로 다른 행렬입니다. 가중치 행렬 $W$와 $W’$는 학습 전 굉장히 작은 랜덤한 값을 초기값으로 갖습니다. CBOW에서는 이 가중치 행렬 $W$와 $W’$를 업데이트 하면서 학습이 이루어집니다.

3.3 CBOW 계산 과정

CBOW의 계산 과정에 대해 살펴보겠습니다.

예를 들어 코퍼스에 아래와 같은 문장이 있다고 가정해봅시다.

예문 : “The fat cat sat on the mat”

CBOW는 주변에 있는 단어들로 중간에 있는 단어들을 예측하는 방법이므로, “The”, “fat”, “cat”, “on”, “the”, “mat”으로부터 “sat”을 예측하고자 합니다. 이때 윈도우 크기를 2로 설정하면, 중심 단어는 “sat”, 주변 단어는 “fat”, “cat”, “on”, “the”가 됩니다.

먼저 주변 단어들의 one-hot vector들과 가중치 행렬을 곱하여 embedded vector들을 구합니다.

$V = x \times W$
  • $x$ : 각 주변 단어의 one-hot vector ($1 \times V = 1 \times 7$ 벡터)
  • $W$ : 가중치 행렬 ($V \times M = 7 \times 5$ 행렬)
  • $V$ : embedded vector ($1 \times M = 1 \times 5$ 벡터)

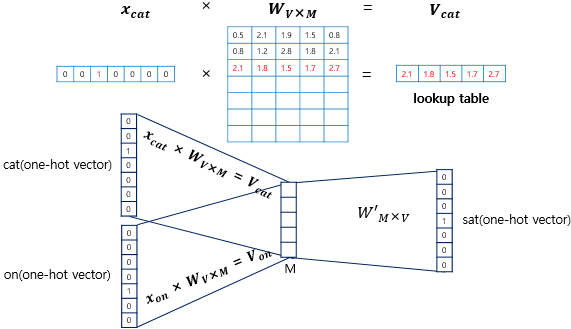
이때 $x$는 각각 $i$번째 인덱스에서는 1을, 이외에는 0을 값으로 갖는 one-hot vector들이기 때문에 $x$와 $W$를 곱하는 것은 사실상 행렬 $W$의 $i$번째 행을 그대로 읽어오는 것과 동일합니다. 즉 가중치 행렬 $W$에서 해당 주변 단어에 해당되는 행 벡터를 참조(lookup)해오는 것입니다. 이러한 작업을 룩업 테이블(lookup table)이라고 부릅니다.

이러한 과정을 그림으로 나타내면 다음과 같습니다.

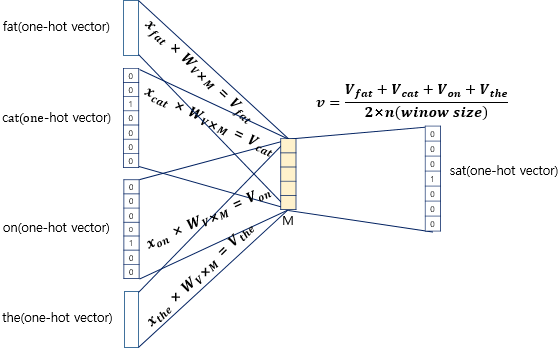
다음으로 embedded vector들에 대하여 평균을 내 평균 벡터를 구합니다.

$v = \frac{V_1 + V_2 + \cdots + V_{2n}}{2 \times n}$
  • $V$ : embedded vector
  • $v$ : embedded vector들의 평균 벡터
  • $n$ : 윈도우 크기

이를 그림으로 나타내면 다음과 같습니다.

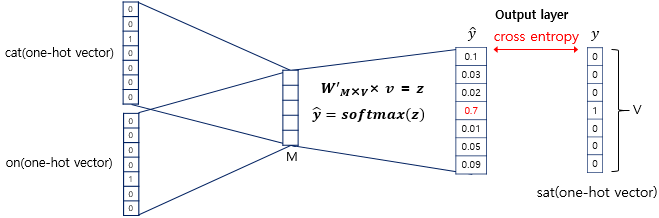
그러고 나서 평균 벡터와 가중치 행렬을 곱하여 score vector를 구합니다.

$z = v \times W'$
  • $v$ : 평균 벡터 ($1 \times M = 1 \times 5$ 벡터)
  • $W’$ : 가중치 행렬 ($M \times V = 5 \times 7$ 행렬)
  • $z$ : score vector ($1 \times V = 1 \times 7$ 벡터)

마지막으로 score vector에 소프트맥스 함수를 취하여 확률값을 구합니다.

$\hat{y} = softmax(z)$


$\hat{y}$는 score vector에 소프트맥스 함수를 취한 것으로, 각 원소가 0과 1 사이의 값을 갖고 모든 원소의 총합은 1이 되어 확률값을 나타내게 됩니다. 다시 말해 $\hat{y}$에서 $j$번째 인덱스가 갖는 0과 1사이의 값은 $j$번째 단어가 중심 단어일 확률을 의미합니다. CBOW의 경우 주변 단어들로 중심 단어를 예측하기 때문에 $\hat{y}$는 1개 나옵니다.

이를 그림으로 나타내면 다음과 같습니다.

3.4. CBOW 학습 과정

이제 CBOW의 파라미터 학습 과정을 살펴보고자 합니다.

CBOW에서는 손실 함수(loss function)로 cross-entropy 함수를 사용합니다. 이를 식으로 나타내면 다음과 같습니다.

$H \left( \hat{y}, y \right) = - \sum_{j=1}^{\lvert V \rvert} y_j \log \left( \hat{y}_j \right)$


그런데 $y_j$는 one-hot vector이므로 모든 원소에 대한 sum은 결국 하나의 원소에 대해서만 계산됩니다. 따라서 위 식은 다음과 같이 간단하게 표현할 수 있습니다.

$H \left( \hat{y}, y \right) = - y_j \log \left( \hat{y}_j \right)$


결론적으로, CBOW에서는 아래의 식을 최소화 하는 방향으로 학습을 진행합니다.

$H \left( \hat{y}, y \right) = - \sum_{j=1}^{\lvert V \rvert} y_j \log \left( \hat{y}_j \right)$


학습이 끝나면 행렬 $W$의 각 행 또는 행렬 $W’$의 각 열을 각 단어의 임베딩 벡터로 사용합니다.

4. Skip-Gram

4.1. Skip-Gram 개념

Skip-gram은 중간에 있는 단어들로 주변에 있는 단어들을 예측하는 방법입니다. 이를 위해 중심 단어로 주변 단어를 예측합니다. Skip-gram에서의 중심 단어(center word), 주변 단어(context word), 윈도우 크기 (window size)는 다음과 같습니다.

  • 중심 단어 (centor word) : 예측하는 데에 사용되는 단어
  • 주변 단어 (context word) : 예측하고자 하는 단어
  • 윈도우 크기 (window size) : 앞뒤로 몇 개의 단어들을 주변 단어로 볼 것인지
    • 즉 윈도우 크기가 $n$이면 앞쪽의 단어 $n$개와 뒤쪽의 단어 $n$개 총 $2n$개의 주변 단어들을 예측

슬라이딩 윈도우 (Sliding Window)

Skip-gram에서는 윈도우를 계속 움직이면서 중심 단어와 주변 단어 선택을 바꿔감으로써 학습을 위한 데이터셋을 만듭니다. 이를 슬라이딩 윈도우(sliding window)라고 합니다.

예를 들어 코퍼스에 아래와 같은 문장이 있다고 가정해봅시다.

예문 : “The fat cat sat on the mat”

이때 슬라이딩 윈도우는 다음과 같이 이루어집니다.

4.2. Skip-gram 아키텍처

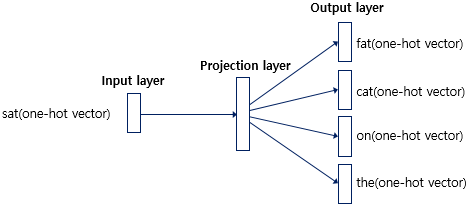
Skip-gram의 아키텍처는 다음과 같습니다.

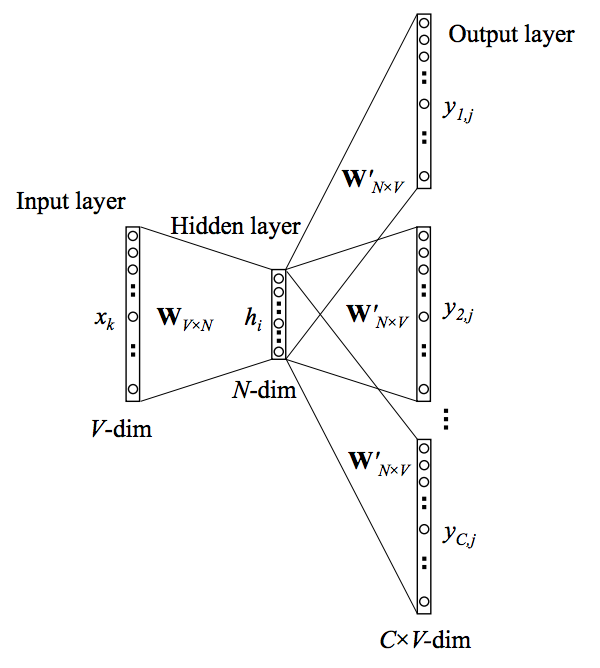
위 그림에서 $V$는 one-hot vector의 차원을, $N$은 사용자가 설정한 embedded vector의 차원을 의미합니다.

  • $V$ : one-hot vector의 차원
  • $N$ : embedded vector의 차원 (사용자 설정)

Skip-gram은 입력층(Input layer), 은닉층(Hidden layer), 출력층(Output layer)을 갖습니다. 각각의 차원은 다음과 같습니다.

  • 입력층 : $V$ 차원
  • 은닉층 : $N$ 차원
  • 출력층 : $C \times V$ 차원

입력층에는 중심 단어의 원-핫 벡터가, 출력층에는 사용자가 설정한 윈도우 크기 내 주변 단어들의 원-핫 벡터가 필요합니다. 은닉층(Hidden layer)은 투사층(Projection layer)이라고 불리기도 하는데, 룩업 테이블(Lookup table) 연산을 수행합니다.

Skip-gram에서 학습해야 하는 파라미터는 가중치 행렬 $W$와 $W’$입니다.

  • $W$ : 입력층과 은닉층 사이의 가중치 행렬 ($V \times N$ 행렬)
  • $W’$ : 은닉층과 출력층 사이의 가중치 행렬 ($N \times V$ 행렬)

이때 가중치 행렬 $W$와 $W’$는 같은 행렬을 전치(transpose)한 것이 아니라 서로 다른 행렬입니다. 가중치 행렬 $W$와 $W’$는 학습 전 굉장히 작은 랜덤한 값을 초기값으로 갖습니다. Skip-gram에서는 이 가중치 행렬 $W$와 $W’$를 업데이트 하면서 학습이 이루어집니다.

4.3. Skip-gram 계산 과정

Skip-gram의 계산 과정에 대해 살펴보겠습니다.

먼저 중심 단어의 one-hot vector와 가중치 행렬을 곱하여 embedded vector를 구합니다.

$v = x \times W$
  • $x$ : 중심 단어의 one-hot vector ($1 \times V$ 벡터)
  • $W$ : 가중치 행렬 ($V \times M$ 행렬)
  • $v$ : embedded vector $1 \times M$ 벡터

Skip-gram에서는 embedded vector가 하나이기 때문에 평균을 구하지 않습니다.

그러고 나서 embedded vector와 가중치 행렬을 곱하여 score vector를 구합니다.

$z = v \times W'$
  • $v$ : embedded vector ($1 \times M$ 벡터)
  • $W’$ :가중치 행렬 ($ M \times V$ 행렬)
  • $z$ : score vector ($1 \times V$ 벡터)

마지막으로 score vector에 소프트맥스 함수를 취하여 확률값을 구합니다.

$\hat{y} = softmax(z)$


$\hat{y}$는 score vector에 소프트맥스 함수를 취한 것으로, 각 원소가 0과 1 사이의 값을 갖고 모든 원소의 총합은 1이 되어 확률값을 나타내게 됩니다. 다시 말해, $\hat{y}$에서 $j$번째 인덱스가 갖는 0과 1사이의 값은 $j$번째 단어가 중심 단어일 확률을 의미합니다.

Skip-Gram의 경우 중심 단어로 주변 단어들을 예측하기 때문에 $\hat{y}$는 아래와 같이 $2n$개 나옵니다.

$\hat{y}_{c−n}, \cdots, \hat{y}_{c−1}, \hat{y}_{c+1}, \cdots, \hat{y}_{c+n}$


이를 실제 주변 단어들의 one-hot vector들과 비교합니다.

$y^{(c−n)}, \cdots, y^{(c−1)}, y^{(c+1)}, \cdots, y^{(c+n)}$

5. 참고자료

Efficient Estimation of Word Representations in Vector Space

댓글남기기

참고