[NLP] RNN (Recurrenct Neural Networks) ; 순환 신경망
이 글은 RNN의 개념, 구조, 순전파, 역전파, 그리고 파이토치를 활용한 RNN 구현에 관한 기록입니다.
1. RNN의 개념
RNN(Recurrent Neural Network)은 순환 구조를 갖고 있는 인공신경망 중 하나입니다. RNN은 hidden layer의 결과를 output layer 방향으로 보내면서 동시에 다시 hidden layer 방향으로 보낸다는 특징을 갖고 있습니다. 이 역할을 하는 것이 바로 셀(cell)입니다.

위 그림에서 셀은 A로 표현되어 있습니다. 이때 셀이 output layer 방향으로 혹은 hidden layer 즉 다음 시점의 자신에게 보내는 값을 hidden state라고 합니다. 셀은 각각의 시점(time step)에서 바로 이전 시점에서의 hidden state를 자신의 입력(input)으로 사용하는 재귀적 활동을 합니다. 다시 말해 $t$시점의 셀은 $t$시점의 hidden state 값을 계산하기 위한 입력(input)으로 $t-1$시점의 셀이 보낸 $t-1$시점의 hidden state 값을 사용합니다. 이를 통해 이전 단계에서 다음 단계로 정보가 전달되는 것이 가능하게 됩니다.
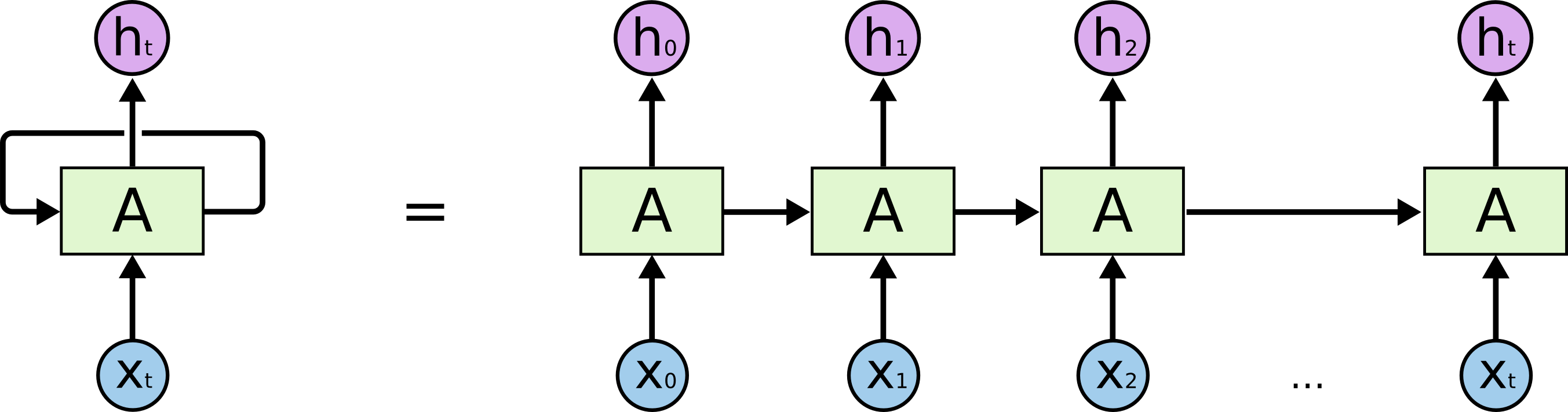
위 그림에서 볼 수 있듯이, RNN은 순서 혹은 시간을 고려할 수 있다는 특징을 갖습니다. 따라서 RNN은 음성, 문자 등 순차적으로 등장하는 데이터를 처리하는 데에 유용합니다.
2. RNN의 활용
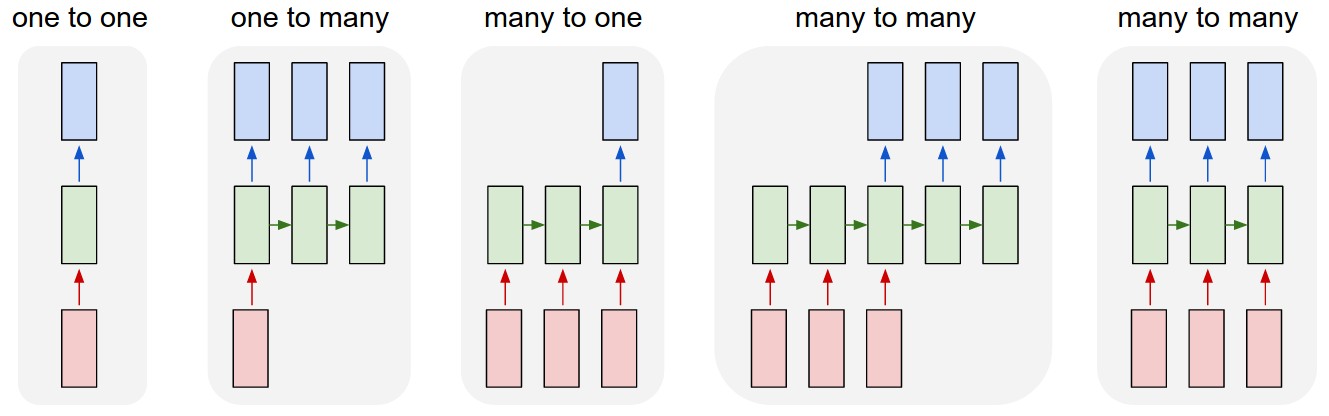
- one to many : Image captioning
- input : 이미지
- output : 단어들 = 문장
- many to one : Sentiment Analysis (감성 분석) = Sentiment Classification (감성 분류)
- input : 단어들 = 문장
- output : 긍정/부정을 나타내는 감성 점수
- many to many : Machine Translation (기계 번역)
- input : 단어들 = 문장
- output : 단어들 = 문장
3. RNN의 구조
RNN의 기본 구조는 다음과 같습니다.
- $x_t$ : 현재 시점 $t$에서의 input
- $h_{t-1}$ : 이전 시점 $t-1$에서의 hidden state 값
- $h_t$ : 현재 시점 $t$에서의 hidden state 값
- $y_t$ : 현재 시점 $t$에서의 output
- $W_x$ : input layer에서 input 값을 위한 가중치
- $W_h$ : 이전 시점 $t-1$의 hidden state 값인 $h_{t−1}$을 위한 가중치
- $W_y$ : output layer에서 output 값을 위한 가중치
hidden layer 연산
hidden layer는 input $x_t$과 이전 시점의 hidden state $h_{t-1}$를 입력받아 hidden state $h_t$를 출력합니다. 이때 활성화함수로 하이퍼볼릭탄젠트 함수를 사용합니다.
$ hidden \ layer \ : \ h_t = \tanh \left( W_h h_{t−1} + W_x x_t + b \right) $
- $h_t$ : 현재 시점 $t$에서의 hidden state 값
- $h_{t-1}$ : 이전 시점 $t-1$에서의 hidden state 값
- $W_h$ : 이전 시점 $t-1$의 hidden state 값인 $h_{t−1}$을 위한 가중치
- $x_t$ : 현재 시점 $t$에서의 input
- $W_x$ : input layer에서 input 값을 위한 가중치
가중치 $W_x$, $W_h$, $W_y$는 모든 시점에서 각각의 값을 동일하게 공유합니다. 물론 hidden layer가 2개 이상일 경우, 각 hidden layer에서의 가중치 값은 서로 다릅니다.
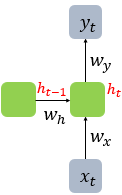
hidden layer 연산을 그림으로 표현하면 다음과 같습니다.
- $d$ : input 즉 단어 벡터의 차원
-
$D_h$ : hidden state의 크기
- $h_{t-1}$ : $( D_h \times 1 )$
- $W_h$ : $( D_h \times D_h )$
- $x_t$ : $( d \times 1 )$
- $W_x$ : $( D_h \times d )$
- $b$ : $( D_h \times 1 )$
output layer 연산
$ output \ layer \ : \ y_t = f \left( W_y h_t + b \right) $
- $y_t$ : 현재 시점 $t$에서의 output
- $h_t$ : 현재 시점 $t$에서의 hidden state 값
- $W_y$ : output layer에서 output 값을 위한 가중치
output layer에서는 활성화함수로 비선형 활성화함수를 사용합니다. binary class 분류 문제의 경우에는 시그모이드 함수를, multi class 분류 문제의 경우에는 소프트맥스 함수를 사용합니다.
4. RNN의 순전파
문자 수준(character level)의 언어 모델(Language Model)을 생각해봅시다. 예를 들어, RNN 모델에 “hello”를 학습시켜 “hell”을 넣으면 “o”를 예측하여 결과적으로 “hello”를 출력하도록 하고자 합니다.
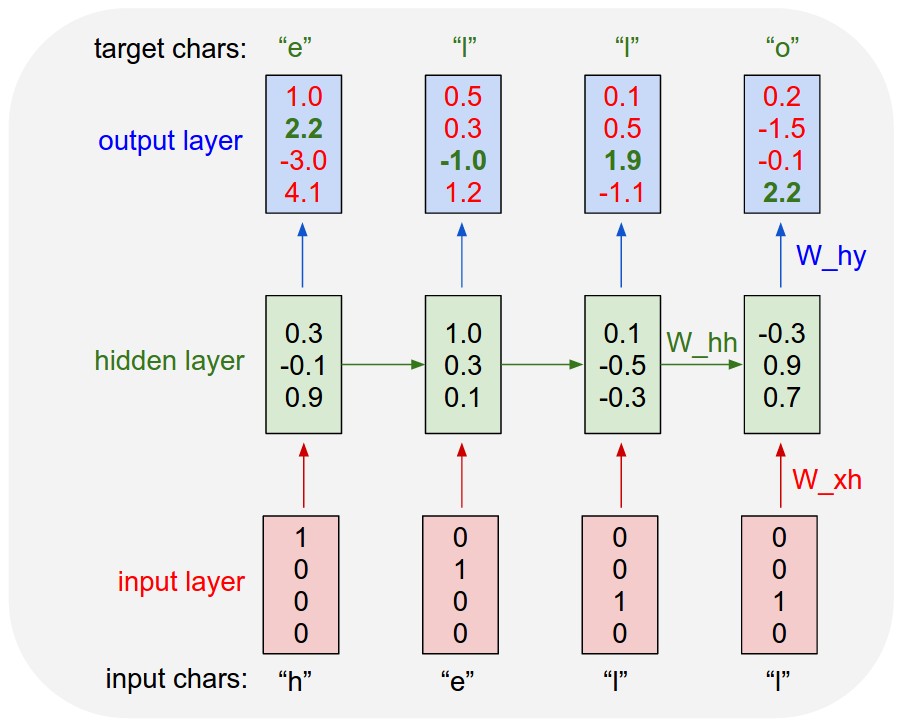
먼저 각 문자 “h”, “e”, “l”, “o”를 원-핫 벡터 $[1,0,0,0], \ [0,1,0,0], \ [0,0,1,0], \ [0,0,0,1]$로 표현합니다. 첫번째 input $x_1$은 “h”를 나타내는 원-핫 벡터 $[1,0,0,0]$입니다. 이를 바탕으로 $h_1$인 $[0.3,−0.1,0.9]$를 만듭니다. 이때 $h_0$는 존재하지 않기 때문에 랜덤으로 값을 설정합니다. 이를 바탕으로 $y_1$인 $[1.0,2.2,−3.0,4.1]$를 만듭니다. 두번째, 세번째, 네번째 시점에 대해서도 같은 방식으로 계산합니다. 이 과정을 순전파(foward propagation ; forward pass)라고 합니다.
다른 인공신경망과 마찬가지로 RNN도 학습을 위해서는 정답을 필요로 합니다. 이 예시에서는 다음 문자가 정답이 됩니다. 즉 “h”에 대한 정답은 “e”, “e”에 대한 정답은 “l”, “l”에 대한 정답은 “l”, “l”에 대한 정답은 “o”입니다.
위 그림에서, output $[1.0,2.2,-3.0,4.1]$, $[0.5,0.3,-1.0,-1.1]$, $[0.1,0.5,1.9,-1.1]$, $[0.2,1.5,-0.1,2.2]$ 중 초록색으로 표시된 숫자들은 정답의 인덱스 위치에 있는 숫자들입니다. 따라서 이 초록색으로 표시된 숫자들의 값이 커지는 방향으로 역전파(backpropagation)를 수행하게 됩니다.
RNN에서 학습하는 파라미터는 다음과 같습니다.
- input $x$를 hidden layer $h$로 보내는 $W_{xh}$
- 이전 hidden layer $h$에서 다음 hidden layer $h$로 보내는 $W_{hh}$
- hidden layer $h$에서 output $y$로 보내는 $W_{hy}$
이 파라미터들은 역전파(backpropagation)를 통해 업데이트 됩니다. 그리고 모든 시점의 state에서 이 parameter들은 동일하게 적용됩니다(shared weights).
지금까지 설명한 RNN의 순전파를 도식화하면 다음과 같습니다.
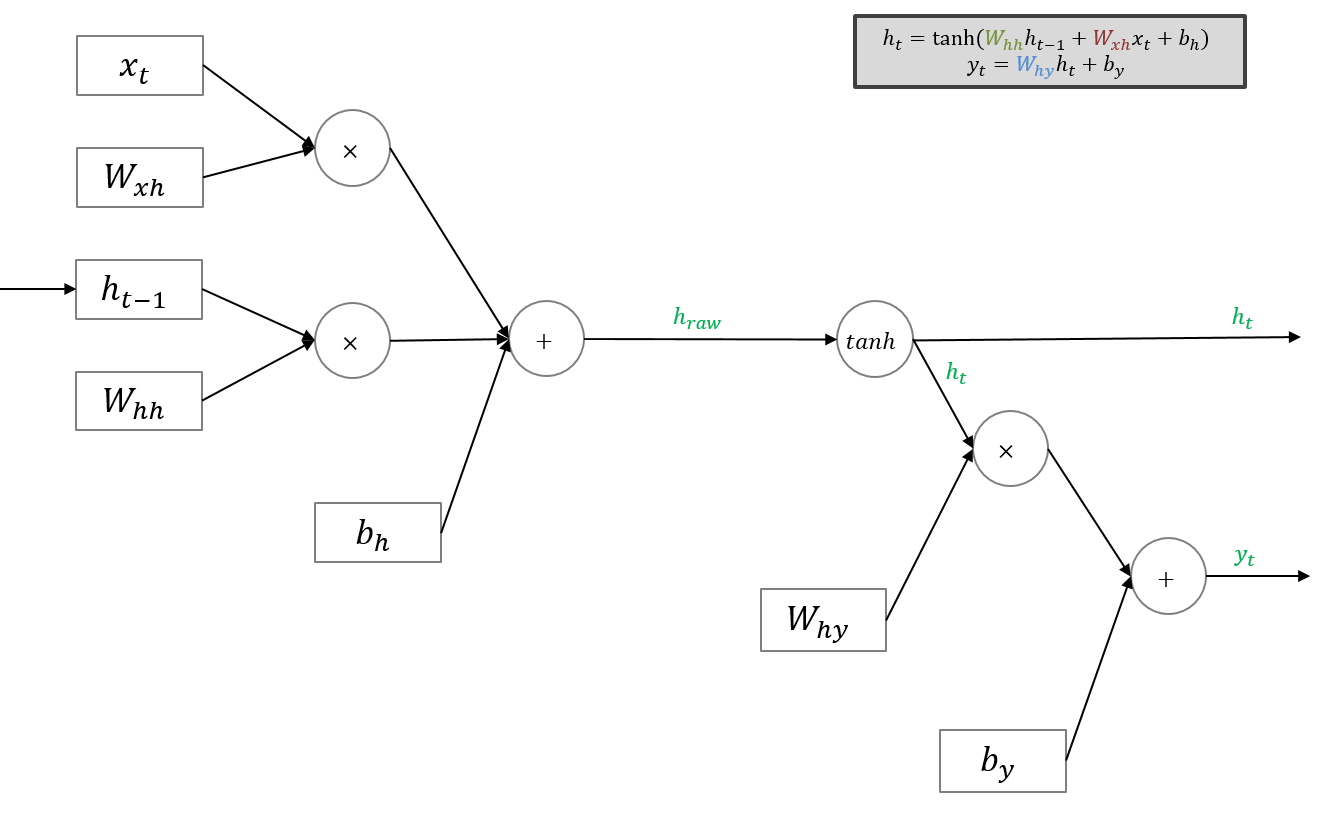
5. RNN의 역전파
RNN의 역전파의 전체적인 과정은 다음과 같습니다.

이를 세부적으로 살펴보겠습니다. RNN에서 학습 parameter는 $W_{xh}$, $W_{hh}$, $W_{hy}$입니다.

순전파 과정을 따라 최종 출력되는 결과는 $y_t$입니다. 따라서 RNN의 역전파 연산에서 가장 먼저 등장하는 것은 최종 Loss에 대한 $y_t$의 그래디언트 ${dL \over dy_t}$입니다. 이를 편의상 $dy_t$라고 표기합니다. $dy_t$는 덧셈 그래프를 타고 양방향에 모두 전달됩니다. $dW_{hy}$는 흘러들어온 그래디언트 $dy_t$에 로컬 그래디언트 $h_t$를 곱하여 구합니다. $dh_t$는 흘러들어온 그래디언트 $dy_t$에 $W_{hy}$를 곱하여 구합니다. $dh_{raw}$는 흘러들어온 그래디언트인 $d_{ht}$에 로컬 그래디언트인 $1 − \tanh^2 ( h_{raw} )$을 곱하여 구합니다. 나머지도 동일한 방식으로 구할 수 있습니다.
다만 아래의 그림에 주의할 필요가 있습니다.
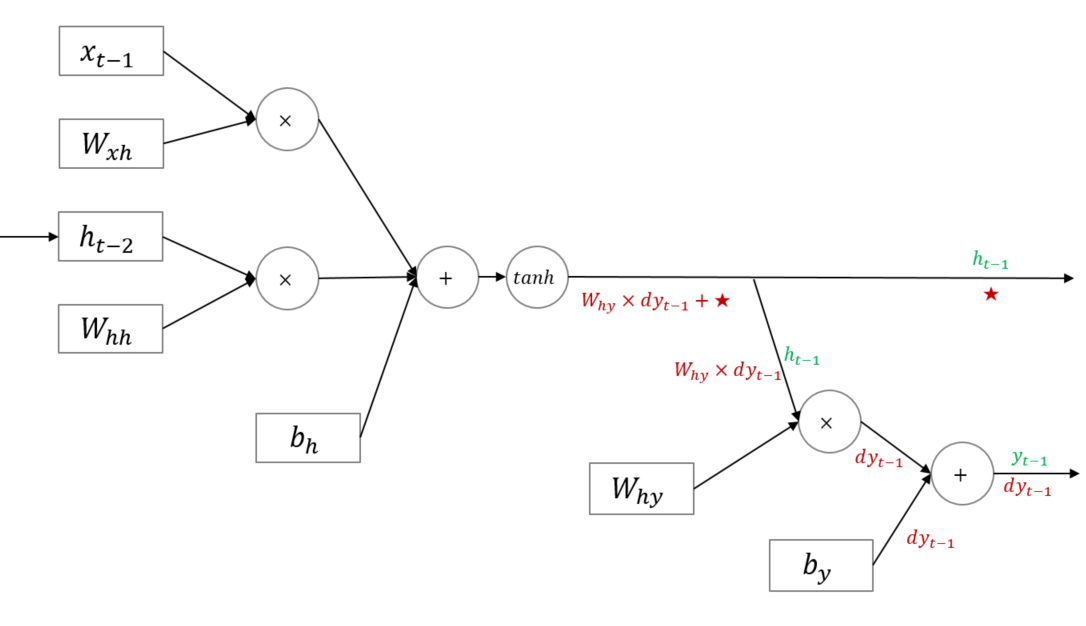
RNN은 hidden state가 순환 구조를 띄는 신경망입니다. 즉 $h_t$를 만들 때 $h_{t−1}$가 반영됩니다. 이는 $dh_{t−1}$를 구할 때 $t-1$ 시점의 Loss에서 흘러들어온 그래디언트인 $W_{hy} \times dy_{t−1}$ 뿐만 아니라 $\bigstar$에 해당하는 그래디언트 또한 더하여 동시에 반영된다는 것을 의미합니다. 따라서 $W_{xh}$, $W_{hh}$ 학습을 위한 그래디언트를 계산할 때에는 시점(time step)에 유의해야 합니다. (Back-Propagation Trough Time ; BPTT)
6. RNN의 장기의존성 문제 (The Problem of Long-Term Dependencies)
RNN의 매력 중 하나는 이전의 정보를 현재의 task에 연결할 수 있다는 아이디어입니다. 하지만 이에 있어 RNN은 상황에 따라 다른 성능을 나타냅니다. 예를 들어, 이전 단어들을 바탕으로 다음 단어를 예측하는 언어 모델을 생각해봅시다.
현재의 task를 수행하기 위해 최근의 정보만을 필요로 하는 경우가 존재합니다. 만약 “the clouds are in the sky”라는 텍스트에서 마지막 단어 “sky”를 예측하고자 한다고 가정해봅시다. 최근의 정보 “the clouds are in the”를 통해 다음 단어가 “sky”일 것이라는 사실이 거의 명백하기 때문에, 더 이상의 어떠한 문맥도 필요하지 않습니다.
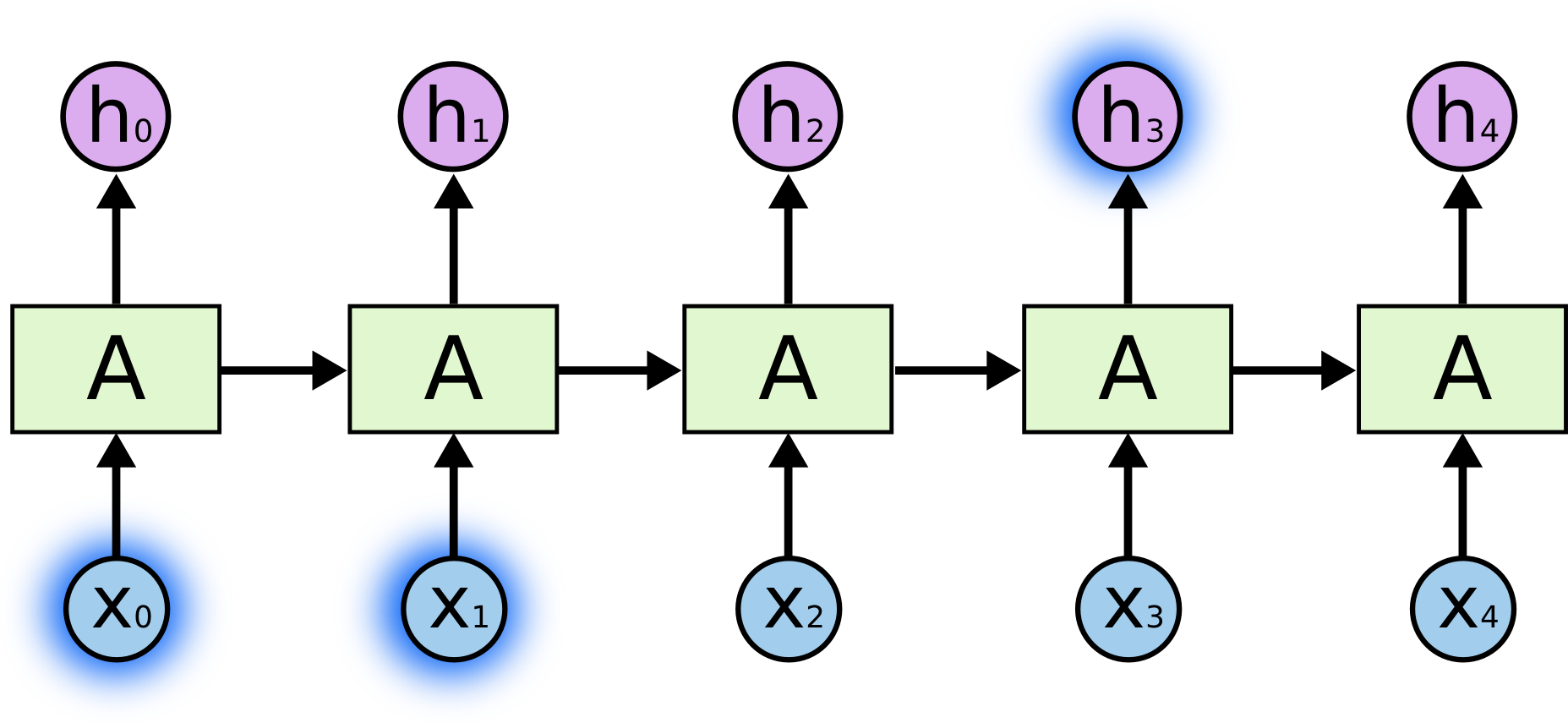
이러한 경우, 즉 위 그림과 같이 관련 정보와 관련 정보가 필요한 시점 사이의 거리가 가까운 경우, RNN의 학습 능력에는 큰 문제가 없습니다.
그러나, 현재의 task를 수행하기 위해 최근의 정보 그 이상의 문맥을 필요로 하는 경우도 존재합니다. 만약 “I grew up in France… I speak fluent French.”라는 텍스트에서 마지막 단어 “French”를 예측하고자 한다고 가정해봅시다. 최근의 정보 “I speak fluent”를 통해서는 다음 단어가 언어의 이름일 것이라고만 예측할 수 있기 때문에, 이를 어떠한 언어인지로 좁히고 싶다면 훨씬 더 이전의 정보인 “France”라는 문맥이 필요합니다.
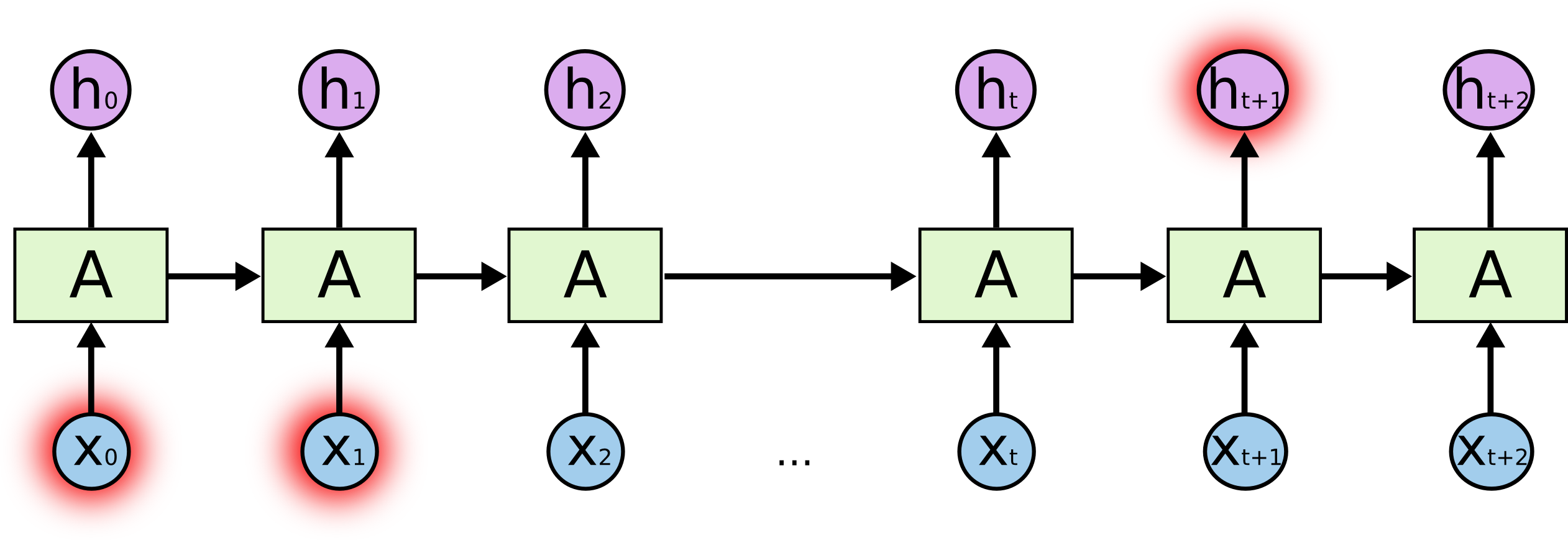
이러한 경우, 즉 위 그림과 같이 관련 정보와 관련 정보가 필요한 시점 사이의 거리가 먼 경우, RNN의 학습 능력은 크게 저하됩니다.
이를 RNN의 장기의존성 문제(The Problem of Long-Term Dependencies)라고 합니다. 이론적으로는 RNN이 장기의존성(long-term dependencies)을 다룰 수 있습니다. 매개변수(parameters)를 신중하게 설정하면 됩니다. 하지만, 현실에서는 RNN이 이를 학습할 수 없는 것으로 보입니다.
이 문제를 해결하기 위해 고안된 것이 바로 LSTM입니다.
6. RNN Code
Settings
import numpy as np
import torch
import torch.nn as nn
import torch.optim as optim
sentences = ["i like dog", "i love coffee", "i hate milk", "you like cat", "you love milk", "you hate coffee"]
dtype = torch.float
Text Preprocessing
word_list = list(set(" ".join(sentences).split())) # 중복되는 단어들을 제거하여 리스트 생성
word_dict = {w: i for i, w in enumerate(word_list)} # word를 key로, index를 value로 갖는 딕셔너리 생성
number_dict = {i: w for i, w in enumerate(word_list)} # index를 key로, word를 value로 갖는 딕셔너리 생성
n_class = len(word_dict)
print(number_dict)
{0: 'milk',
1: 'you',
2: 'dog',
3: 'like',
4: 'coffee',
5: 'hate',
6: 'i',
7: 'love',
8: 'cat'}
TextRNN Parameter
batch_size = len(sentences)
n_step = 2 # 학습 하려고 하는 문장의 길이 - 1
n_hidden = 5 # 은닉층 사이즈
def make_batch(sentences):
input_batch = []
target_batch = []
for sen in sentences:
word = sen.split()
input = [word_dict[n] for n in word[:-1]]
target = word_dict[word[-1]]
input_batch.append(np.eye(n_class)[input]) # One-Hot Encoding
target_batch.append(target)
return input_batch, target_batch
input_batch, target_batch = make_batch(sentences)
input_batch = torch.tensor(input_batch, dtype=torch.float32, requires_grad=True)
target_batch = torch.tensor(target_batch, dtype=torch.int64)
TextRNN
class TextRNN(nn.Module):
def __init__(self):
super(TextRNN, self).__init__()
self.rnn = nn.RNN(input_size=n_class, hidden_size=n_hidden, dropout=0.3)
self.W = nn.Parameter(torch.randn([n_hidden, n_class]).type(dtype))
self.b = nn.Parameter(torch.randn([n_class]).type(dtype))
self.Softmax = nn.Softmax(dim=1)
def forward(self, hidden, X):
X = X.transpose(0, 1)
outputs, hidden = self.rnn(X, hidden)
outputs = outputs[-1] # 최종 예측 Hidden Layer
model = torch.mm(outputs, self.W) + self.b # 최종 예측 최종 출력 층
return model
Training
model = TextRNN()
# Loss & Optimizer
criterion = nn.CrossEntropyLoss()
optimizer = optim.Adam(model.parameters(), lr=0.01)
# Training
for epoch in range(500):
hidden = torch.zeros(1, batch_size, n_hidden, requires_grad=True)
output = model(hidden, input_batch)
loss = criterion(output, target_batch)
if (epoch + 1) % 100 == 0:
print('Epoch:', '%04d' % (epoch + 1), 'cost =', '{:.6f}'.format(loss))
optimizer.zero_grad()
loss.backward()
optimizer.step()
input = [sen.split()[:2] for sen in sentences]
hidden = torch.zeros(1, batch_size, n_hidden, requires_grad=True)
predict = model(hidden, input_batch).data.max(1, keepdim=True)[1]
print([sen.split()[:2] for sen in sentences], '->', [number_dict[n.item()] for n in predict.squeeze()])
Epoch: 0100 cost = 0.574982
Epoch: 0200 cost = 0.127370
Epoch: 0300 cost = 0.047592
Epoch: 0400 cost = 0.025828
Epoch: 0500 cost = 0.016676
[['i', 'like'], ['i', 'love'], ['i', 'hate'], ['you', 'like'], ['you', 'love'], ['you', 'hate']] -> ['dog', 'coffee', 'milk', 'cat', 'milk', 'coffee']


댓글남기기