[NLP] 언어 모델 (Language Model)

언어 모델(Language Model; LM)은 언어라는 현상을 모델링 하고자 단어 시퀀스 또는 문장에 확률을 할당(assign)하는 모델입니다. 언어 모델에는 크게 통계를 이용한 방법과 인공신경망을 이용한 방법이 있습니다.

1. Statistical Languagel Model : 통계를 이용한 방법
2. N-gram Language Model : 통계를 이용한 방법
3. Neural Network Language Model : 인공신경망을 이용한 방법

1. 언어 모델 (Language Model ; LM)

LM 개념

언어 모델(Language Model)은 단어 시퀀스에 확률을 할당(assign)하는 모델입니다. 단어 시퀀스에 확률을 할당하기 위해 사용하는 방법으로는, 이전 단어들이 주어졌을 때 다음 단어를 예측하도록 하는 방법과 양쪽 단어들이 주어졌을 때 가운데 비어있는 단어를 예측하도록 하는 방법이 있습니다. 이번 포스팅에서 다루는 언어 모델들은 모두 전자에 속하고, 후자에 속하는 언어 모델로는 BERT가 있습니다.

따라서 언어 모델링(Language Modeling)은 주어진 이전 단어들로부터 다음 단어를 예측하는 작업을 말합니다. 이를 조건부 확률을 이용하여 표현해보고자 합니다.

먼저, 이전 단어들이 주어졌을 때 다음 단어의 등장 확률은 다음과 같습니다. 즉, $n-1$개의 이전 단어들이 주어졌을 때 다음 $n$번째 단어의 확률은 다음과 같습니다.

$P(w_n \mid w_1, \cdots, w_{n−1})$

또, 하나의 단어를 $w$, 단어 시퀀스을 $W$라고 할 때, $n$개의 단어가 등장하는 단어 시퀀스 $W$의 확률은 다음과 같습니다.

$P \left( W \right) = P \left( w_1, w_2, w_3, w_4, w_5, …, w_n \right)$

마지막으로, 전체 단어 시퀀스 $W$의 확률은 모든 단어가 예측되고 나서야 알 수 있으므로 전체 단어 시퀀스 즉 문장의 확률은 다음과 같습니다.

$P(W) = P(w_1, w_2, w_3, w_4, w_5, \cdots, w_n) = \prod_{i=1}^n P(w_n \mid w_1, \cdots, w_{n−1})$

LM 활용 분야

언어 모델은 주로 자연어 생성(Natural Language Generation ; NLG)에 사용됩니다. 언어 모델은 다음과 같이 단어 시퀀스에 확률을 할당함으로써 보다 적절한 문장을 판단합니다.

• 기계 번역 (Machine Translation)
  • $P(나는 \ 버스를 \ 탔다) > P(나는 \ 버스를 \ 태운다)$
  • 언어 모델은 두 문장을 비교하여 왼쪽 문장의 확률이 더 높다고 판단합니다.
• 오타 교정 (Spell Correction)
  • 선생님이 교실로 부리나케 $P(달려갔다) > P(잘려갔다)$
  • 언어 모델은 두 문장을 비교하여 왼쪽 문장의 확률이 더 높다고 판단합니다.
• 음성 인식 (Speech Recognition)
  • $P(나는 \ 메롱을 \ 먹는다) < P(나는 \ 메론을 \ 먹는다)$
  • 언어 모델은 두 문장을 비교하여 오른쪽 문장의 확률이 더 높다고 판단합니다.

2. 통계적 언어 모델 (Statistical Language Model ; SLM)

통계적 언어 모델(Statistical Language Model ; SLM)은 언어 모델의 전통적인 접근 방법으로, 통계를 이용하여 언어를 모델링 하는 방법입니다.

SLM 개념

조건부 확률은 두 확률 $P \left(A \right), P \left( B \right)$에 대하여 다음과 같은 관계를 갖습니다.

$P \left( B \mid A \right) = \frac{P \left( A,B \right)}{P \left( A \right)}$

$P \left( A, B \right) = P \left( A \right) P \left( B \mid A \right)$

이를 바탕으로, 조건부 확률은 $n$개의 확률에 대하여 다음과 같은 관계를 갖습니다.

$P \left( x_1, x_2, x_3, …, x_n \right) = P \left( x_1 \right) P \left( x_2 \mid x_1 \right) P \left( x_3 \mid x_1, x_2 \right) … P \left( x_n \mid x_1…x_{n−1} \right)$

이를 조건부 확률의 연쇄 법칙(chain rule)이라고 합니다. 조건부 확률의 연쇄 법칙(chain rule)을 활용해보면, 문장의 확률은 이전 단어들이 주어졌을 때 각 단어들이 다음 단어로 등장할 확률의 곱으로 표현됩니다.

$P \left( w_1, w_2, w_3, w_4, w_5, …, w_n \right) = \prod_{i=1}^n P \left( w_n \mid w_1, …, w_{n−1} \right)$

예를 들어, 문장 “An adorable little boy is spreading smiles”이 있다고 가정해봅시다. 이 문장의 확률 $P \left( An \ adorable \ little \ boy \ is \ spreading \ smiles \right)$은 다음과 같습니다.

$P \left( An \ adorable \ little \ boy \ is \ spreading \ smiles \right) = P \left( An \right) \times P\left( adorable \mid An \right) \times P \left(little \mid An \ adorable \right)$
$\times \ P \left( boy \mid An \ adorable \ little \right) \times P \left( is \mid An \ adorable \ little \ boy \right) \times P \left( spreading \mid An \ adorable \ little \ boy \ is\right)$
$\times \ P \left( smiles \mid An \ adorable \ little \ boy \ is \ spreading \right)$

즉 문장의 확률은 각 단어에 대한 예측 확률들을 곱함으로써 구할 수 있습니다.

그렇다면 이전 단어들이 주어졌을 때 각 단어들이 다음 단어로 등장할 확률은 어떻게 구할까요? SLM에서는 다음 단어에 대한 예측 확률을 구하기 위해서 카운트 기반의 접근을 사용합니다. 즉 SLM에서는 이전 단어들이 주어졌을 때 다음 단어의 등장 확률을 카운트에 기반하여 계산합니다.

예를 들어, “An adorable little boy”가 나왔을 때 “is”가 나올 확률 $P \left( is \mid An \ adorable \ little \ boy \right)$는 다음과 같습니다.

$P \left( is \mid An \ adorable \ little \ boy \right) = \frac{count \left( An \ adorable \ little \ boy \ is \right)}{count \left(An \ adorable \ little \ boy \right)}$

만약 코퍼스에서 “An adorable little boy”가 등장하는 횟수가 100번이고 “An adorable little boy” 다음에 “is”가 등장하는 횟수는 30번이면, $P \left( is \mid An \ adorable \ little \ boy \right) = 0.3$입니다.

3. N-gram 언어 모델 (N-gram Language Model ; N-gram LM)

N-gram 언어 모델(N-gram Language Model ; N-gram LM)은 통계를 이용하여 언어를 모델링 하는 방법입니다. SLM의 일종이기에 카운트 기반의 접근을 사용합니다. 하지만 이전에 등장한 모든 단어들을 고려하는 SLM과는 달리, N-gram LM은 일부 단어들만을 고려합니다.

N-gram LM 개념

N-gram LM은 다음 단어를 예측하고자 할 때 예측하고자 하는 단어 이전의 $n-1$개의 단어들을 가지고 카운트에 기반하여 계산합니다. N-gram은 n개의 연속적인 단어 시퀀스로, 몇 개의 단어를 포함하여 카운트 할 것인지를 결정하는 기준이 됩니다.

예를 들어, 아래와 같은 문장이 있다고 가정해봅시다.

예문 : “An adorable little boy is spreading smiles”

이때 각 n에 대한 n-gram은 다음과 같습니다.

• 1-gram : unigram : “an”, “adorable”, “little”, “boy”, “is”, “spreading”, “smiles”
• 2-gram : bigram : “an adorable”, “adorable little”, “little boy”, “boy is”, “is spreading”, “spreading smiles”
• 3-gram : trigram : “an adorable little”, “adorable little boy”, “little boy is”, “boy is spreading”, “is spreading smiles”
• 4-gram : “an adorable little boy”, “adorable little boy is”, “little boy is spreading”, “boy is spreading smiles”

예를 들어, “An adorable little boy”가 나왔을 때 “is”가 나올 확률을 구하려고 합니다. SLM에서는 이를 다음과 같이 계산합니다.

$P \left( is \mid An \ adorable \ little \ boy \right) = \frac{count(An \ adorable \ little \ boy \ is)}{count(An \ adorable \ little \ boy)}$

한편 N-gram LM에서는 이를 다음과 같이 계산합니다. ($n=3$)

$P \left( is \mid An \ adorable \ little \ boy \right) \approx P \left( is \mid little \ boy \right) = \frac{count(little \ boy \ is)}{count(little \ boy)}$

즉, SLM에서는 예측하고자 하는 단어 이전의 모든 단어들을 포함하여 카운트 하지만, N-gram LM에서는 예측하고자 하는 단어 이전의 몇몇 단어들만을 포함하여 카운트 한 뒤 이를 근사합니다. 이로써 코퍼스에서 해당 단어 시퀀스를 카운트 할 확률이 높아집니다.

N-gram LM 한계

• 여전히 희소 문제 (Sparsity Problem)가 존재합니다.
• n을 선택하는 데에 있어 trade-off 문제가 존재합니다.
  • n을 작게 선택하면, 모델의 성능이 떨어집니다.
  • n을 크게 선택하면, 모델이 무거워지고 희소 문제가 심각해집니다.
• 모델의 성능이 코퍼스의 분야(domain)에 따라 달라집니다.

4. 피드 포워드 신경망 언어 모델 (Neural Network Language Model ; NNLM)

피드 포워드 신경망 언어 모델(Neural Network Language Model, NNLM)은 신경망 언어 모델의 시초로, 인공신경망을 이용하여 언어를 모델링 하는 방법입니다.

NNLM 개념

NNLM은 단어 간 유사도를 학습하도록 함으로써 이전 단어들이 주어졌을 때 보다 더 정확하게 다음 단어를 예측할 수 있도록 합니다. 이를 통해 희소 문제(sparsity problem)을 해결할 수 있습니다.

NNLM 구조

NNLM의 구조에 대해 알아보고자 합니다. 예를 들어 코퍼스에 아래와 같은 문장이 있다고 가정해봅시다.

예문 : “what will the fat cat sit on”

언어 모델링에 앞서 모든 단어들에 대하여 원-핫 인코딩을 진행합니다.

what = [1, 0, 0, 0, 0, 0, 0]
will = [0, 1, 0, 0, 0, 0, 0]
the = [0, 0, 1, 0, 0, 0, 0]
fat = [0, 0, 0, 1, 0, 0, 0]
cat = [0, 0, 0, 0, 1, 0, 0]
sit = [0, 0, 0, 0, 0, 1, 0]
on = [0, 0, 0, 0, 0, 0, 1]

이러한 각 단어의 원-핫 벡터들은 NNLM의 입력(input)이자 레이블(label)이 됩니다. 언어 모델은 이전 단어들이 주어졌을 때 다음 단어를 예측하는 모델이므로, “what will the fat cat”이 입력으로 주어지면 다음 단어 “sit”을 예측하는 방식으로 학습이 진행됩니다. 이는 실제로는 “what”, “will”, “the”, “fat”, “cat”의 원-핫 벡터를 입력받아 “sit”의 원-핫 벡터를 예측하는 문제가 됩니다. 이때 NNLM에서는 다음 단어를 예측하기 위해 이전 모든 단어들을 참고하는 것이 아니라 $n$개의 단어들만을 참고하는데, 이 $n$을 윈도우 크기(window size)라고 합니다. 즉 $n=4$일 때, “sit”을 예측하기 위해 4개의 단어 “will”, “the”, “fat”, “cat”만을 참고한다는 것입니다.

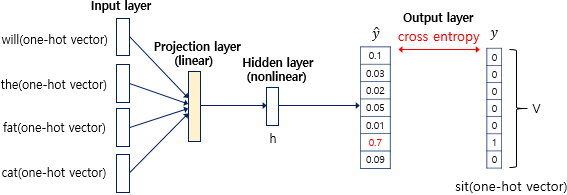
NNLM의 전체적인 구조는 다음과 같습니다.

NNLM은 입력층(Input layer), 투사층(Projection layer), 은닉층(Hidden layer), 출력층(Output layer) 총 4개의 층(layer)로 이루어져 있습니다. 각각의 차원은 다음과 같습니다.

• 입력층 : $V$차원
• 투사층 : $M$차원 (linear layer)
• 은닉층 : $h$차원 (nonlinear layer)
• 출력층 : $V$차원

입력층에서는 각 단어의 원-핫 벡터들을 입력으로 받습니다. 윈도우 크기 $n=4$이므로, 입력은 4개의 단어 “will”, “the”, “fat”, “cat” 각각의 원-핫 벡터가 됩니다.

투사층에서는 입력층의 출력인 원-핫 벡터를 입력받아 가중치 행렬과 곱한 후 이를 연결하여 출력합니다. 이를 식으로 나타내면 다음과 같습니다.

$projection \ layer : p^{layer} = (lookup(x_{t−n}) ; \cdots ; lookup(x_{t−2}) ; lookup(x_{t−1})) = (e_{t−n} ; \cdots ; e_{t−2} ; e_{t−1})$

• $x$ : 각 단어의 원-핫 벡터
• $t$ : 예측하고자 하는 단어의 인덱스
• $n$ : 윈도우의 크기

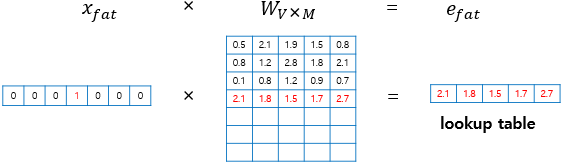
예를 들어, 원-핫 벡터의 차원이 7이고 투사층의 차원이 5이면, $1 \times 7$ 크기의 원-핫 벡터와 $7 \times 5$ 크기의 가중치 행렬을 곱하여 $1 \times 5$ 크기의 임베딩 벡터를 만듭니다.

• $x$ : 각 단어의 원-핫 벡터 (크기는 $1 \times V$)
• $W$ : 가중치 행렬 (크기는 $V \times M$)
• $e$ : 각 단어의 임베딩 벡터 (크기는 $1 \times M$)
• $V$ : 단어 집합의 크기
• $M$ : 투사층의 크기

$x$가 각각 $i$번째 인덱스에서는 1을, 이외에는 0을 값으로 갖는 원-핫 벡터라는 점에서, 원-핫 벡터 $x$와 가중치 행렬 $W$를 곱하는 것은 행렬 $W$의 $i$번째 행을 그대로 읽어오는 것(lookup)과 동일합니다. 이러한 작업을 룩업 테이블(Lookup table)이라고 부릅니다. 그 결과 $1 \times V$ 크기를 갖는 원-핫 벡터 $x$는 $1 \times M$ 크기를 갖는 임베딩 벡터 $e$로 바뀌어 더 작은 차원을 가질 수 있게 됩니다. 임베딩 벡터들은 학습 전 랜덤한 값을 초기값을 갖고, 학습이 진행됨에 따라 값이 업데이트 됩니다.

각 단어의 원-핫 벡터를 룩업 테이블을 통해 임베딩 벡터로 변경하고 나면, 모든 임베딩 벡터들의 값을 연결(concatenation)합니다. 그 결과 투사층의 출력의 크기는 $n \times M$이 됩니다.

은닉층에서는 투사층의 출력을 입력받아 가중치를 곱하고 편향을 더하여 활성화 함수를 지난 것을 출력합니다. 은닉층의 크기는 $h$입니다. 이를 식으로 나타내면 다음과 같습니다.

$hidden layer : h^{layer} = \tanh( W_h p^{layer} + b_h)$

• $W_h$ : 가중치
• $b_h$ : 편향
• $\tanh$ : 활성화 함수

이를 그림으로 나타내면 다음과 같습니다.

출력층에서는 은닉층의 출력을 입력받아 가중치를 곱하고 편향을 더하여 활성화 함수를 지난 것을 출력합니다. 출력층의 크기는 $V$입니다. 이를 식으로 나타내면 다음과 같습니다.

$output layer : \hat{y} = softmax(W_y h^{layer} + b_y)$

• $W_y$ : 가중치
• $b_y$ : 편향
• $softmax$ : 활성화 함수

출력층에서는 활성화 함수로 소프트맥스(softmax) 함수를 사용하는데, 그 결과 각 원소는 0과 1 사이의 값을 갖고 모든 원소의 총합은 1이 되어 확률값을 나타내게 됩니다. 즉 벡터 $\hat{y}$에서 $j$번째 인덱스가 갖는 0과 1사이의 값은 $j$번째 단어가 다음 단어일 확률을 의미합니다. 따라서 예측값 $\hat{y}$은 실제값 $y$ 즉 다음 단어의 원-핫 벡터에 가까워져야 합니다. NNLM에서는 $\hat{y}$와 $y$가 가까워지는 방향으로 학습을 진행하기 위해 손실 함수(loss function)로 cross-entropy 함수를 사용합니다. 이를 바탕으로 역전파가 이루어지면서 가중치 행렬과 임베딩 벡터에 대하여 학습이 진행됩니다.

이를 그림으로 나타내면 다음과 같습니다.

NNLM 의의 및 한계

• 의의
  • NNLM은 단어 간 유사도를 표현할 수 있는 임베딩 벡터 즉 밀집 벡터(dense vector)를 활용하여 기존 언어 모델의 희소 문제(sparsity problem)를 해결합니다.
  • NNLM에서는 모든 n-gram을 저장하지 않아도 되기 때문에 N-gram LM에 비해 저장 공간에 있어 효율적입니다.
• 한계
  • NNLM은 N-gram LM과 마찬가지로 다음 단어를 예측하기 위해 이전 모든 단어들을 참고하는 것이 아니라 정해진 $n$개의 단어들만을 참고한다는 점에서 한계가 존재합니다.
  • 코퍼스 내 각 문장들의 길이가 서로 다를 수 있음에도 불구하고 입력의 길이가 고정되어야 한다(fixed-length input)는 점에서 문제가 발생합니다.

5. 참고자료

딥 러닝을 이용한 자연어 처리 입문