[NLP] 어텐션 메커니즘 (Attention Mechanism)

이 글은 어텐션의 개념, 구조, 종류에 관한 기록입니다.

1. 어텐션의 등장 배경

Sequence-to-Sequence 모델은 source language를 입력(input)받아 벡터로 만들어 출력(output)하는 인코더(Encoder)와 인코더가 출력한 벡터를 입력(input)받아 target language를 출력(output)하는 디코더(Decoder)로 구성됩니다. 이러한 Sequence-to-Sequence 모델에는 문제점이 존재합니다.

1. 하나의 고정된 크기의 벡터에 모든 정보를 압축하려고 하여 정보 손실이 발생합니다.
2. 장기의존성 문제(The Problem of Long-Term Dependencies), 즉 기울기 소실(Vanishing Gradient) 문제가 있습니다.

이는 결국 source language와 target language의 길이가 길어질수록 모델의 성능이 나빠지는 결과를 초래합니다. 이러한 문제를 해결하고자 기계 번역(Machine translation)을 위한 Sequence-to-Sequence 모델에 어텐션 (Attention) 메커니즘이 도입됩니다.

2. 어텐션의 핵심 아이디어

어텐션 메커니즘 (Attention Mechanism) 의 핵심 아이디어는 바로 “중요한 부분에 집중(attention)”하는 것입니다. 즉, source sentence 전체가 아니라 source sentece 일부에 집중한다는 것입니다. 예를 들어 “I am a student”라는 영어 문장을 “je sus étudiant”라는 프랑스어 문장으로 번역하는 Sequence-to-Sequence 모델이 있다고 가정해봅시다. 이때 “중요한 부분에 집중(attention)”한다는 어텐션의 핵심 아이디어는 “étudiant”를 예측할 때 “student”에 집중(attention)한다는 것입니다. 어텐션 메커니즘은 인코더가 “student”를 입력받아 만든 벡터 즉 인코더 output이 디코더가 “étudiant”를 예측할 때 사용하는 벡터 즉 디코더 input과 유사할 것이라고 가정합니다.

3. 어텐션의 구조

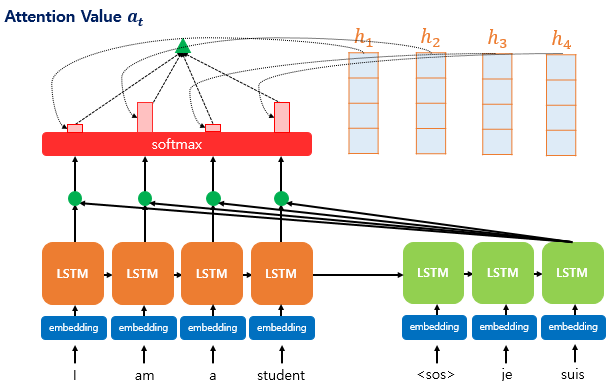
“I am a student”라는 영어 문장을 입력으로 받아 “je sus étudiant”라는 프랑스어 문장으로 출력하는 어텐션 매커니즘을 예로 들어 어텐션 매커니즘의 구조를 이해해보고자 합니다. target sentece의 첫번째 단어 “je”와 두번째 단어 “sus”는 이미 예측한 상태를 가정합니다. 이제 target sentece의 세번째 단어인 “étudiant”를 예측해야 합니다. 이때 어텐션의 전체적인 구조는 다음과 같습니다.

• 주황색 네모 : 인코더 (Encoder)
• 연두색 네모 : 디코더 (Decoder)
• 초록색 동그라미 : 어텐션 스코어 (Attention score)
• 빨간색 네모 : 어텐션 분포 (Attention distribution)
• 빨간색 막대 : 어텐션 가중치 (Attention weight)
• 초록색 세모 : 어텐션 값 (Attention value)

이제 각 단계 별로 자세히 살펴보도록 하겠습니다.

1. 어텐션 스코어 (Attention Score) 계산

• $h_1, h_2, h_3, h_4$ : 시점 1, 2, 3, 4에서의 인코더의 hidden state
• $s_t$ : 현재 시점 $t$에서의 디코더의 hidden state

어텐션 메커니즘에는 여러 종류가 있는데, 그중 Dot product attention을 사용하고자 합니다. Dot product attention에서는 어텐션 스코어를 계산하기 위해 디코더의 hidden state인 $s_t$를 전치한 $s_t^T$와 인코더의 hidden state인 $h_1, h_2, h_3, h_4$의 내적(dot product)을 수행합니다. 즉 디코더 hidden state $s_t$와 인코더 hidden state $h_i$에 대한 어텐션 스코어 함수는 다음과 같습니다.

$score(s_t, h_i) = s_t^T h_i$

이때 어텐션 스코어 $e^t$는 다음과 같습니다.

$e^t = [ s_t^T h_1, \ldots, s_t^T h_N ]$

즉, 어텐션 스코어는 디코더의 hidden state와 인코더의 hidden state 각각이 얼마나 유사한지를 나타내는 스칼라 값입니다.

2. 어텐션 분포 (Attention Distribution) 계산

위 그림에서 빨간색 막대 각각은 어텐션 가중치(Attention Weight)를, 빨간색 막대 전체는 어텐션 분포(Attention Distribution)을 나타냅니다. 어텐션 분포 $\alpha_t$는 어텐션 스코어 $e_t$에 소프트맥스 함수를 적용하여 구할 수 있습니다.

$\alpha_t = softmax(e_t)$

모든 어텐션 가중치 값의 합은 1로, 어텐션 분포가 확률 분포임을 알 수 있습니다. 또 각각의 어텐션 가중치는 확률 값입니다.

3. 어텐션 값 (Attention Value) 계산

각 어텐션 가중치 값과 각각의 인코더의 hidden state를 곱한 후 모두 더하여 즉 가중합(weighted sum)을 하여 어텐션 값 (Attention Value) $a_t$를 구할 수 있습니다.

$ a_t = \sum_{i=1}^N \alpha_i^t h_i $

이때 어텐션 값은 Attention Output 혹은 Context Vector라고도 합니다.

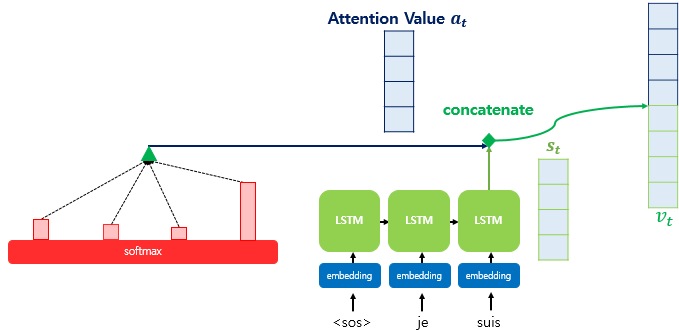
4. 어텐션 값과 디코더의 $t$ 시점의 hidden state 결합(concatenate)

어텐션 값 $a_t$와 디코더의 $t$ 시점의 hidden state인 $s_t$를 결합(concatenate)하여 하나의 벡터 $v_t$로 만듭니다.

$v_t = [ \alpha_t ; s_t ]$

보통은 이 $v_t$를 output layer의 입력(input)으로 사용하는데, 논문에서는 $v_t$를 output layer로 보내기 전 하이퍼볼릭탄젠트 layer를 추가합니다.

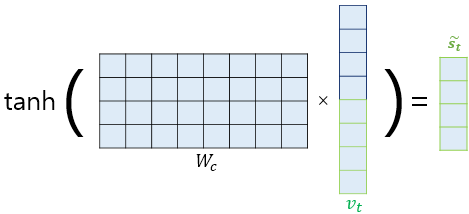
가중치 행렬을 $v_t$에 곱한 후에 하이퍼볼릭탄젠트 함수를 통과하도록 하여 새로운 벡터 $\tilde{s}_t$를 만듭니다.

$\tilde{s}_t = \tanh ( W_c [ \alpha_t ; s_t ] + b_c )$

• $W_c$ : 학습 가능한 가중치 행렬
• $b_c$ : 편향

즉, $t$시점의 hidden state인 $s_t$가 output layer의 입력(input)인 어텐션 메커니즘을 사용하지 않는 seq2seq와 달리, 어텐션 메커니즘에서는 output layer의 입력(input)으로 $\tilde{s}_t$를 사용하여 예측 벡터 $\hat{y}$을 얻습니다.

$\hat{y}_t = softmax ( W_y \tilde{s}_t + b_y )$

어텐션 디코더 계산 과정 정리

• 인코더 hidden state : $h_1, …, h_N \in \mathbb{R}^h$
• 디코더 hidden state : $s_t \in \mathbb{R}^h$

1. 어텐션 스코어 $\mathbf{e}^t$ 계산 : $\mathbf{e}^t = [ \mathbf{s}_t^T \mathbf{h}_1, …, \mathbf{s}_t^T \mathbf{h}_N ] \in \mathbb{R}^N $

2. 어텐션 분포 $\alpha^t$ 계산 : $\alpha^t = softmax ( \mathbf{e}^t ) \in \mathbb{R}^N$

3. 어텐션 값 $a_t$ 계산 : $a_t = \sum_{i=1}^N \alpha_i^t \mathbf{h}_i \in \mathbb{R}^h $

4. 어텐션 값 $a_t$와 디코더 hidden state $s_t$ 결합 : $[ a_t ; s_t ] \in \mathbb{R}^h$

4. 어텐션의 종류

이름	특징
Dot product attention	$score(s_t, h_i) = s_t^T h_i$
Scaled dot product attention	$score(s_t, h_i) = \frac{s_t^T h_i}{\sqrt{n}}$
General attention = Multiplicative attention	$ score(s_t, h_i) = s_t^T W_a h_i$
Concat attention	$score(s_t, h_i) = W_a^T \tanh(W_b [s_t ; h_i])$
Location−base attention	$\alpha_t = softmax(W_a s_t)$
Additive attention	$e_i = v^T \tanh (W_1 h_i + W_2 s_t)$

• $h_i$ : 인코더 hidden state
• $s_t$ : 디코더 hidden state
• $W_a, W_b$ : 학습 가능한 가중치 행렬(weight matrix)
• $v$ : 가중치 벡터(weight vector)

5. 참고자료

NEURAL MACHINE TRANSLATION BY JOINTLY LEARNING TO ALIGN AND TRANSLATE
cs224n
딥 러닝을 이용한 자연어 처리 입문
ratsgo님의 블로그