[딥러닝] 활성화 함수 (Activation Function)
이 글은 활성화 함수, 특히 비선형 활성화 함수에 관한 기록입니다.
활성화 함수 (Activation function)
딥러닝에서 사용하는 인공신경망들은 일반적으로 이전 레이어로부터 값을 입력받아 “어떠한 함수”를 통과시킨 후 그 결과를 다음 레이어로 출력합니다. 이때 “어떠한 함수” 즉 인공신경망의 은닉층(hidden layer)에 사용되는 함수를 활성화 함수라고 합니다.
활성화 함수의 종류는 다음과 같습니다.
- 이진 활성화 함수 (Binary step activation function)
- 선형 활성화 함수 (Linear activation function)
- 비선형 활성화 함수 (Non-linear activation function)
활성화 함수로 비선형 함수를 사용해야 하는 이유
활성화 함수에는 크게 이진 활성화 함수, 선형 활성화 함수, 비선형 활성화 함수가 있지만, 활성화 함수로 비선형 함수를 사용하는 것이 일반적입니다. 왜냐하면, 은닉층에서 이진 활성화 함수를 활성화 함수로 사용할 경우, 다중 출력이 불가능하다는 문제점이 존재하고, 은닉층에서 선형 활성화 함수를 활성화 함수로 사용할 경우, 역전파가 불가능하고 층(layer)을 깊게 쌓는 의미가 사라진다는 문제점이 존재합니다. 따라서 은닉층에서 비선형 활성화 함수를 활성화 함수로 사용하는 것이 바람직합니다.
비선형 활성화 함수 (Non-linear activation function)
- 시그모이드 함수
- 소프트맥스 함수
- 하이퍼볼릭탄젠트 함수
- ReLU 함수
- leaky ReLU 함수
- PReLU 함수
- ELU 함수
- Maxout 함수
- …
1. 시그모이드 함수 (Sigmoid function = Logit function)
시그모이드 함수는 아래와 같이 정의됩니다.
$\sigma(x) = \frac{1}{1 + e^{-x}} = \frac{e^x}{e^x + 1}$
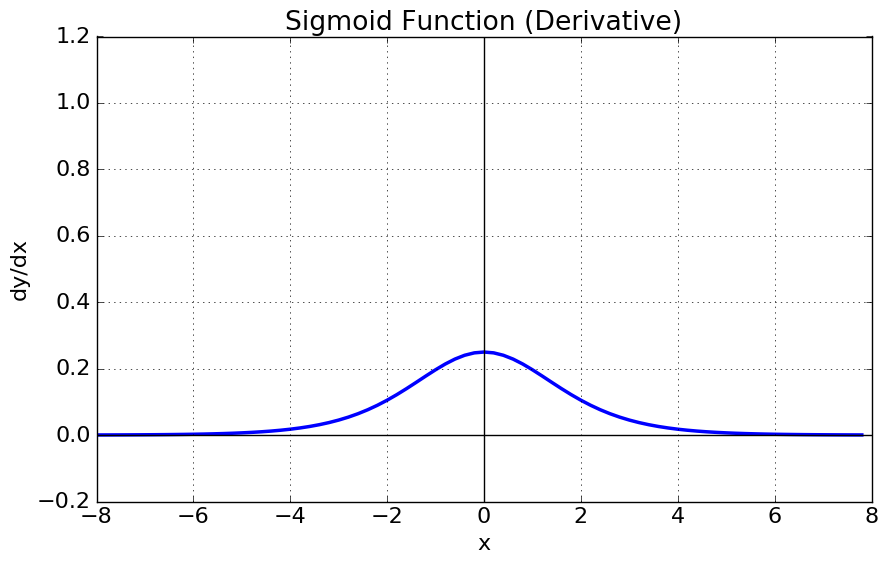
$\sigma’(x) = \sigma(x) (1 - \sigma(x))$
시그모이드 함수의 그래프는 다음과 같습니다.
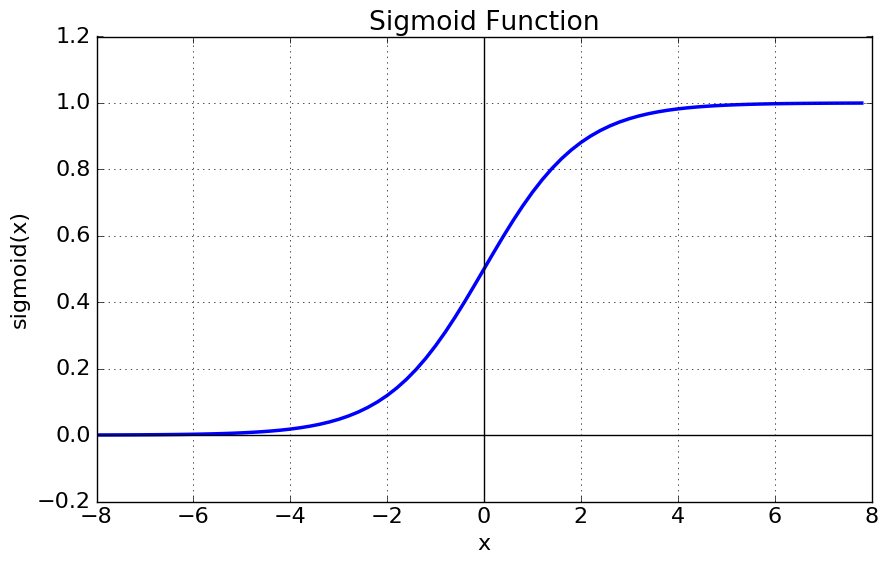
특징
- 출력값이 0과 1 사이입니다.
- 출력값의 중심이 $\frac{1}{2}$입니다. (not zero-centered)
- 입력값이 커질수록 출력값은 1에 가까워지고, 입력값이 작아질수록 출력값은 0에 가까워집니다.
- 입력값이 커질수록/작아질수록 기울기(gradient)는 0에 가까워집니다.
활용
- 이진 분류(binary classification) 문제에서 출력층에 사용합니다.
한계
- Vanishing Gradient 문제가 발생합니다. (학습 성능이 떨어집니다.)
- 이는 시그모이드 함수에서 입력값이 작아질수록/커질수록 기울기(gradient)는 0에 가까워져 기울기가 소실되는 것을 말합니다.
- 학습 속도가 느려질 수 있습니다.
- 출력값의 중심이 0이 아니기 때문에 발생합니다. (not zero-centered)
- exp 함수 사용 시 연산 비용이 큽니다.
2. 소프트맥스 함수 (Softmax function)
소프트맥스 함수는 시그모이드 함수를 일반화 (generalization) 하여 얻을 수 있습니다.
소프트맥스 함수는 아래와 같이 정의됩니다.
$f(x) = \sigma_i (x) = \frac{e^{x_i}}{\sum_j e^{x_j}}$
소프트맥스 함수의 그래프는 다음과 같습니다.
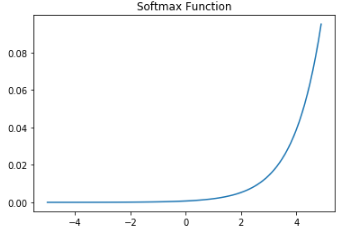
특징
- 출력값이 0과 1 사이입니다.
- 출력값의 총합이 1입니다.
활용
- 다중 클래스 분류(multi-class classification) 문제에서 출력층에 사용합니다.
3. 하이퍼볼릭탄젠트 함수 (Hyperbolic tangent function ; tanh)
하이퍼볼릭탄젠트 함수는 시그모이드 함수를 transformation (-1 vertical shift & 1/2 horizontal squeeze & 2 vertical stretch) 하여 얻을 수 있습니다.
하이퍼볼릭탄젠트 함수는 아래와 같이 정의됩니다.
$\tanh(x) = 2 \sigma (2x) − 1$
$\tanh(x) = \frac{e^x - e^{-x}}{e^x + e^{-x}}$
$\tanh’(x) = 1 − {\tanh}^2 (x)$
하이퍼볼릭탄젠트 함수의 그래프는 다음과 같습니다.
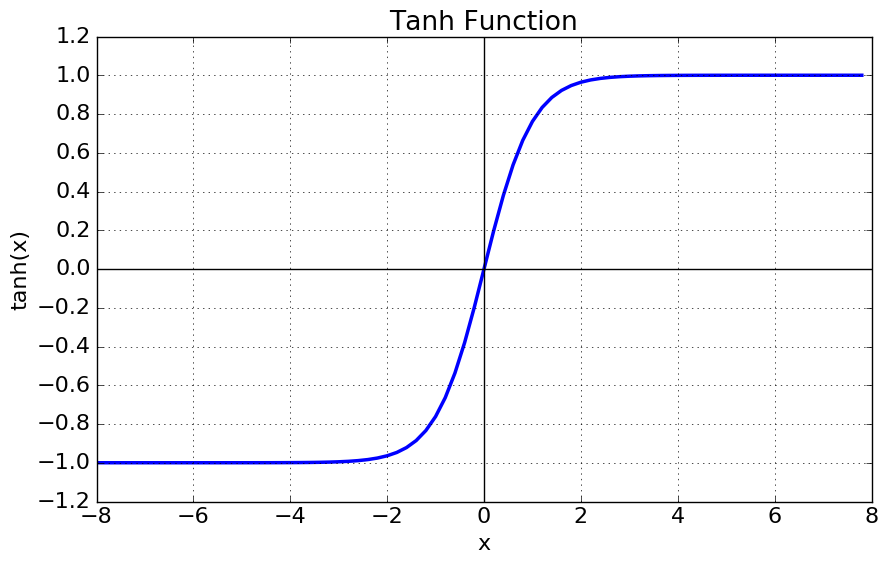
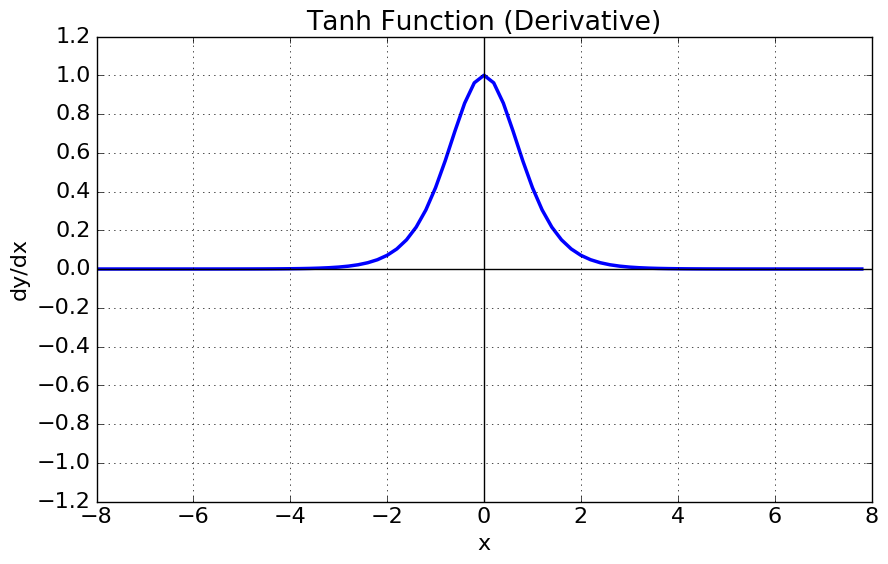
특징
- 출력값이 -1과 1 사이입니다.
- 출력값의 중심이 0입니다. (zero-centered)
- 입력값이 작아질수록 출력값은 0에 가까워지고, 입력값이 커질수록 출력값은 1에 가까워집니다.
- 입력값이 작아질수록/커질수록 기울기(gradient)는 0에 가까워집니다.
의의
- 시그모이드 함수에 비해 학습 성능이 좋습니다.
- 시그모이드 함수의 최적화 과정이 느려지는 문제를 출력값의 중심을 0으로 만듦으로써 해결합니다.
한계
- Vanishing Gradient 문제가 발생합니다.
4. ReLU 함수 (Rectified Linear Unit function ; ReLU)
ReLU 함수는 아래와 같이 정의됩니다.
$f(x) = \max(0, x)$
ReLU 함수의 그래프는 다음과 같습니다.
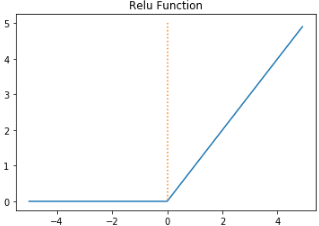
특징
- 입력값이 0보다 작으면 출력값은 0이 되고, 입력값이 0보다 크면 출력값은 $x$가 됩니다.
- 입력값이 0보다 작으면 기울기(gradient)는 0이고, 입력값이 0보다 크면 기울기(gradient)는 1입니다.
의의
- 시그모이드 함수와 하이퍼볼릭탄젠트 함수에 비해 학습 속도가 빠릅니다.
- 연산 비용이 크지 않습니다.
- 구현이 간단합니다.
한계
- Dying ReLU 문제가 발생합니다. (학습 성능이 떨어집니다.)
- Dying ReLU 문제는 ReLu 함수에서 입력값이 0보다 작을 때 기울기(gradient)가 0이 되어 해당 뉴런이 죽는 것을 말합니다.
5. leaky ReLU 함수 (leaky ReLU function ; leaky ReLU)
leaky ReLU 함수는 아래와 같이 정의됩니다.
$f(x) = \max(ax, x)$
이때 $a$는 사용자가 설정하는 하이퍼파라미터입니다. (일반적으로 $a=0.01$)
leaky ReLU 함수의 그래프는 다음과 같습니다.

특징
- 입력값이 0보다 작으면 출력값은 $ax$가 되고, 입력값이 0보다 크면 출력값은 $1$이 됩니다.
- 입력값이 0보다 작으면 기울기(gradient)는 0이고, 입력값이 0보다 크면 기울기(gradient)는 $a$입니다.
의의
- ReLU 함수에 비해 학습 성능이 좋습니다.
- 입력값이 0보다 작을 때 기울기(gradient)가 0이 되는 ReLU 함수와 달리 leaky ReLU 함수에서는 입력값이 0보다 작을 때 기울기(gradient)가 0이 되지 않기 때문입니다.
6. PReLU 함수 (Parametric ReLU function ; PReLU)
PReLU 함수는 다음과 같이 정의됩니다.
$f(x) = \max (\alpha x, x)$
이때 $\alpha$는 학습해야 하는 파라미터입니다.
특징
- 입력값이 0보다 작으면 출력값은 $\alpha x$가 되고, 입력값이 0보다 크면 출력값은 $x$가 됩니다.
- 입력값이 0보다 작으면 기울기(gradient)는 $\alpha$이고, 입력값이 0보다 크면 기울기(gradient)는 $1$입니다.
의의
- 각 레이어마다 적절한 $\alpha$를 학습할 수 있습니다.
7. ELU 함수 (Exponential Linear Unit function ; ELU)
ELU는 함수는 다음과 같이 정의됩니다.
$f(x) = x \quad \quad \quad \quad \ \ if \ x \geq 0$
$f(x) = \alpha (e^x − 1) \quad if \ x < 0$
이때 $\alpha$는 사용자가 설정하는 하이퍼파라미터입니다. (일반적으로 $\alpha=1$)
특징
- 출력값의 중심이 거의 0에 가깝습니다. (zero-centered)
의의
- Dying ReLU 문제를 해결합니다.
한계
- ReLU, leaky ReLU와 달리 exp 함수를 계산해야 해서 연산 비용이 큽니다.
8. Maxout 함수 (Maxout function)
Maxout 함수는 다음과 같이 정의됩니다.
$f(x) = \max( w_1^T x + b_1, w_2^T x + b_2)$
의의
- Dying ReLU 문제를 해결합니다.
한계
- 연산 비용이 큽니다.
- 파라미터의 개수가 두배로 증가하기 때문입니다.
정리
- 활성화 함수로 비선형 함수를 사용합니다.
- ReLU 함수 > ReLU 계열 함수(leaky ReLU, PReLU, ELU 등) > 하이퍼볼릭탄젠트 함수 순으로 시도합니다.
- 시그모이드 함수는 사용하지 않습니다.

댓글남기기